Bresenham's Circle Drawing Algorithm

Bresenham's Circle Drawing Algorithm

As per Eight way symmetry property of circle, circle can be divided into 8 octants each of 45-degrees.
The Algorithm calculate the location of pixels in the first octant of 45 degrees and extends it to the other 7 octants. For every pixel (x, y), the algorithm draw a pixel in each of the 8 octants of the circle as shown below :
Assumption : Center of Cirle is Origin.
Following image illustrates the 8 octants with corresponding pixel:
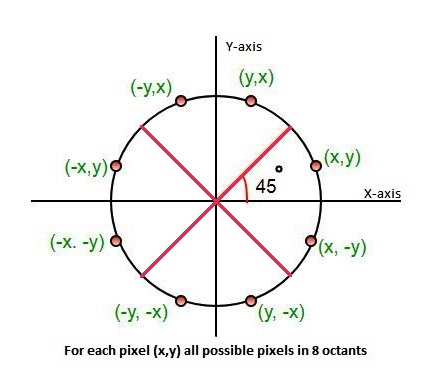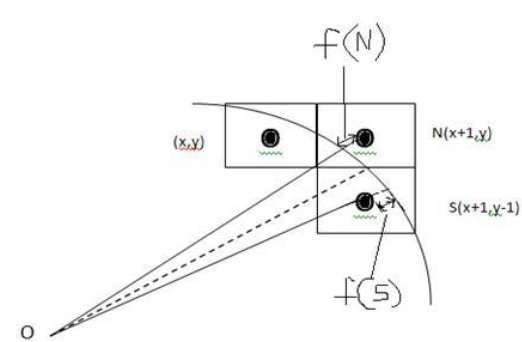
Point (x, y) is in the first octant and is on the circle.
To calculate the next pixel location, can be either:

• N (x+1, y)
• S (x+1, y-1)

It is decided by using the decision parameter d as:

• If d <= 0, then N(x+1, y) is to be chosen as next pixel.
• If d > 0, then S(x+1, y-1) is to be chosen as the next pixel.

Library used: p5.js

Web Editor: https://editor.p5js.org



 Output Screenshots:

 Code:

// initial values
let x, y, r, d, xc, yc;

let i = 0;
let grids = 26;
let scalFact;

function setup() {
  createCanvas(600, 600);
  background(0);

  scalFact = width / grids;
  r = 3 * scalFact;

  xc = 15 * scalFact;
  yc = 8 * scalFact;

  showGrids();
  showRefCircle();
  bresenham();
}

function showGrids() {
  stroke(255);
  for (i; i < grids * scalFact; i += scalFact) {
    line(i, 0, i, height);
    line(0, i, width, i);
  }
}

function showRefCircle() {
  stroke(200);
  noFill();
  circle(xc + (scalFact / 2), yc + (scalFact / 2), r * 2);
}

function bresenham() {
  x = 0;
  y = r;

  d = (3 * scalFact) - (2 * r);

  symPlot();
  while (x <= y) {
    if (d <= 0) {
      d = d + (4 * x) + (6 * scalFact);
    } else {
      d = d + (4 * x) - (4 * y) + (10 * scalFact);
      y -= scalFact;
    }

    x += scalFact;
    symPlot();
  }
}

function symPlot() {
  fillPixel(x + xc, y + yc);
  fillPixel(x + xc, -y + yc);
  fillPixel(-x + xc, -y + yc);
  fillPixel(-x + xc, y + yc);
  fillPixel(y + xc, x + yc);
  fillPixel(y + xc, -x + yc);
  fillPixel(-y + xc, -x + yc);
  fillPixel(-y + xc, x + yc);
}

function fillPixel(x, y) {
  noStroke();
  squareColor = color(255, 255, 255);
  squareColor.setAlpha(100);
  fill(squareColor);
  square(x, y, scalFact);
}